This is an archival copy of the Visualization Group's web page 1998 to 2017. For current information, please vist our group's new web page.
Parallel Stream Surface Computation for Large Data Sets
Problem Statement and Goals
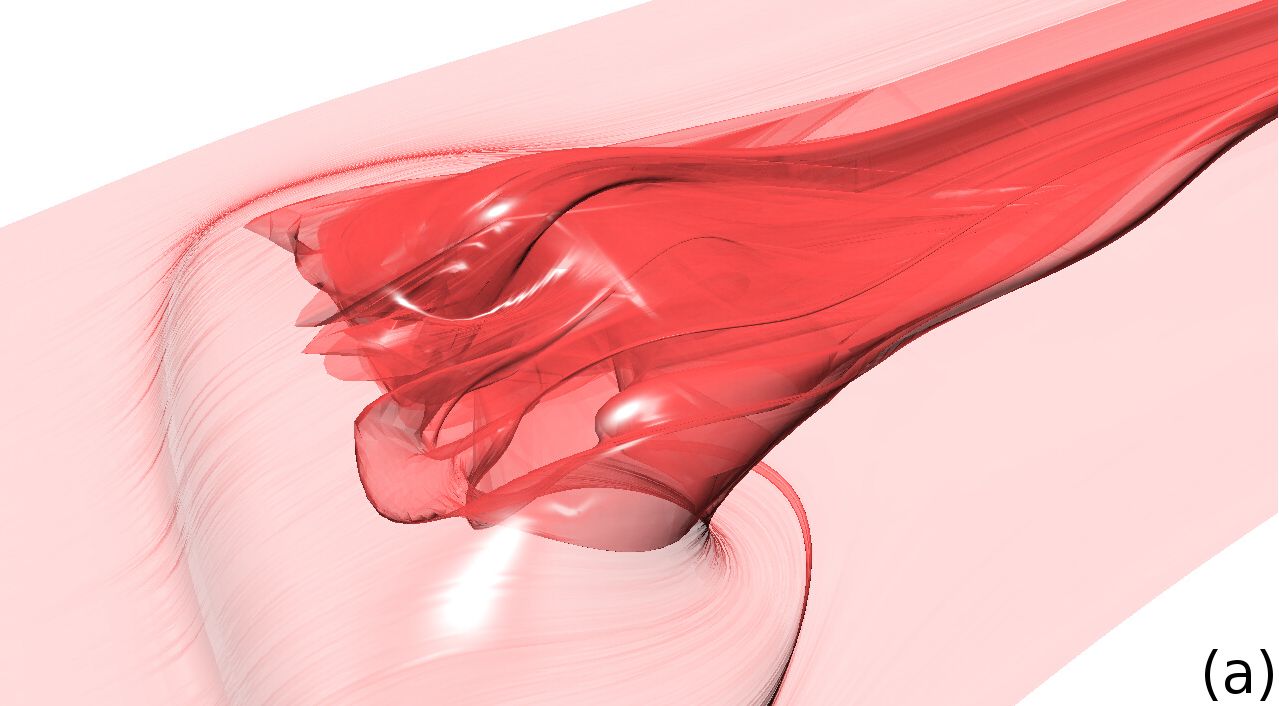
A stream surface is an infinite set of integral curves originating from a seeding curve. It is a powerful visualization tool for gaining insight into characteristics and features of vector fields (see Figure 1 above for an example). In practice, stream surfaces are approximated by using a triangulation of adjacent pairs of integral curves to create the surface. Particles are placed along the seeding curve and advected to create integral curves. When two adjacent integral curves diverge too far, new particles are inserted to adapt the computation and guarantee the accuracy of the approximation. For maximum surface accuracy, especially for long integration times, these new particles must be placed on the initial seeding curve.
Unfortunately, this approach is often not efficient in a distributed-memory parallel environment because the data block containing the new particles is often not readily available to perform further integration. The performance characteristics of stream surface algorithms are different than streamlines and other particle advection-based techniques in two key respects. First, all particles originate along a seeding curve, which results in many data accesses to certain regions of the volume, namely the regions that contain the seeding curve and those in close proximity. Second, the addition of ``refinement particles'' inserted back on the seeding curve results in a fundamentally different data access pattern. In this study, we ask the question: what is the most efficient way to carry out a stream surface calculation on large data, given that its access patterns are different than other particle advection algorithms?
Implementation and Results
An important start to our work is parallelizing the stream surface calculation. Parallelization is necessary for stream surfaces that require more memory than is available on a desktop machine and also to reduce the time spent calculating the surface. This parallelization process goes beyond advecting particles in parallel. We must detect when adjacent integral curves have diverged too far, diminishing the quality of the surface approximation, even when those integral curves reside on different processing elements. Figure 2 below shows the visual results comparing adaptive and non-adaptive stream surface generation techniques. Further, we must be able to create the final surface in a way that guarantees that no processing element exceeds its available memory.
The algorithm we developed supports different approaches for parallelizing particle advection. Efficient parallelization is a challenge since every particle originates on the seeding curve. We study two approaches, parallelizing-over-particle and parallelizing-over-data, and their relative merits in this environment.
Finally, we consider the idea of speculative refinement. Advecting particles is less expensive because the mesh region that a particle traverses is already loaded from disk and in primary cache. Clearly, it would be ideal to know a priori which particles provide a good approximation of the surface. But this is not possible, since the data-dependent nature of the algorithm means that separation of adjacent integral curves must be detected as the particles advect. In short, speculative calculation will advect more particles, but the cost of advecting each particle will be reduced. With this study, we endeavored to assess this balance qualitatively: under what circumstances does speculative calculation of particles improve overall performance? When does speculative calculation stop being beneficial?
Parallel particle advection performance is highly dependent on the initial placement of initial seed points as well as the characteristics of the underlying velocity field. We designed a study that covers a variety of configurations and that determines when the parallelization methods and speculative computation perform best. Specifically, we used three different data sets and varied the size of the seeding curve, the integration time (which affects surface length), and the amount of speculative calculation. The combination of these variables resulted in 120 different experiments.
The study and its results are presented in detail in Camp et al. 2012 (reference below).
Impact
Our research has enabled stream surfaces to be applied to large data sets, which will increase the insight scientists can gain about complex flow phenomena. An implementation will soon be deployed in the VisIt application, which is distributed to a worldwide scientific community.
References
David Camp, Hank Childs, Christoph Garth, Dave Pugmire, and Kenneth I. Joy. Parallel Stream Surface Computation for Large Data Sets. In Proceedings of the IEEE Symposium on Large-Scale Data Analysis and Visualization (LDAV). IEEE Press, 2012. LBNL-5776E.
Contact
David Camp, Hank Childs