This is an archival copy of the Visualization Group's web page 1998 to 2017. For current information, please vist our group's new web page.
Parallel Streamline Calculation
Table of Contents
Introduction
For simulations that involve vector fields, integral curves, or streamlines, are one of the most illuminating techniques to obtain insight; they are a cornerstone of visualization and analysis across a great variety of application domains. Drawing on an intuitive interpretation in terms of particle movement, they are an ideal tool to illustrate and describe a wide range of phenomena encountered in the study of application-domain vector fields, such as transport and mixing in fluid flows.
For a stationary vector field v that does not depend on time, an integral curve is called a streamline and is given by the ordinary differential equation
In the discrete setting we are concerned with here, streamlines are approximated using numerical integration methods to approximate the describing ordinary differential equations. In our streamline implementation, we use an integration scheme of Runge-Kutta type with adaptive stepsize control as proposed by Prince and Dormand (1981). The visualization and analysis of vector fields is an active research area, and so-called integration-based techniques that derive vector field visualization from integral curves have progressed well beyond the direct depiction of individual streamlines or a small subset of them. In particular, we are interested in applications that require tracing a large number of streamlines, thus making parallelization practical
Parallelization Strategies
Compared to isosurface extraction or direct volume rendering, it is difficult to parallelize streamline generation. While it is possible to extract isosurfaces independently within each block of a multi-block data set, or to take samples along a ray within each block independently for volume rendering, it is not possible to extract the portion of a streamline in data blocks independently. This is due to the fact that the streamline depends on the seed point, and for blocks along the path of a streamline it is not known a-priori where on the boundary a streamline enters the block. As a consequence, it is necessary to compute a streamline piece-by-piece, communicating intermediate results between processors as the streamline passes from a blocks owned by a processor to blocks owned by a different processor.
Two extreme parallelization strategies are possible. The first method distributes streamlines to processors. Each streamline remains on the same processor, which load data blocks dynamically as a streamline enters them. This strategy avoids communication and keeps a balanced work load among processors (each processor gets assigned roughly the same number of streamlines). However, in most cases it leads to significant data duplication.
The second method distributes data blocks evenly among processors. Each processors "owns" those streamlines that are currently located in one of its data blocks. This strategy avoids data duplication. However, streamlines need to be communicated from processor to processor as they enter and leave data blocks stored on different processors. Furthermore, this strategy may lead to severe load imbalance if streamlines are distributed unevenly among the data blocks belonging to each processor. VisIt 1.12 implements a third method, which is enabled by default, that uses heuristics to transition its behavior between both methods and attempts minimize data duplication while maintaining an even load balance among processors. In Pugmire (2009) we performed an extensive analysis on the trade offs between the various schemes. In many cases, it is safe to use VisIt's new defaults. However, for a more in-depth understanding, we refer the reader to that paper.
Results
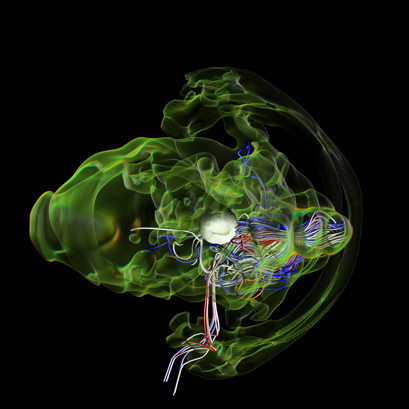
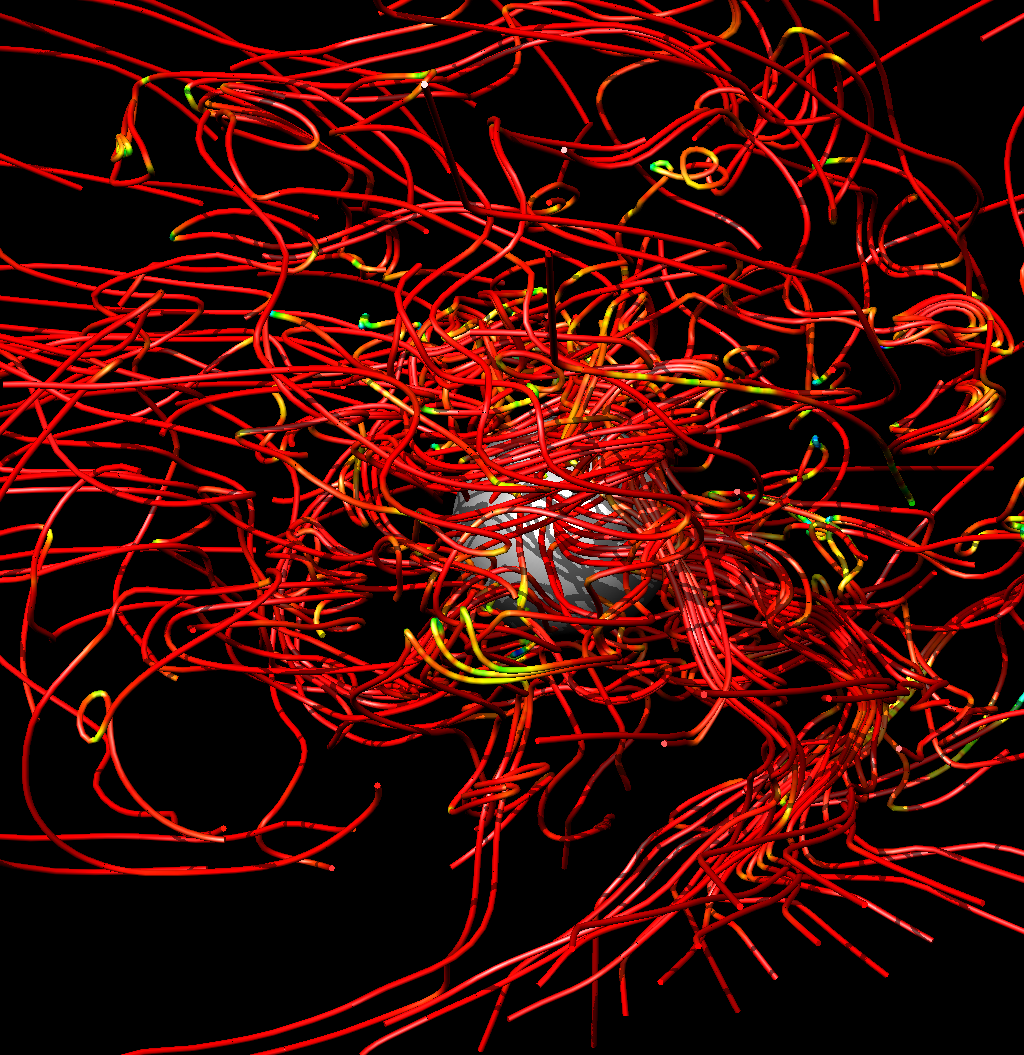

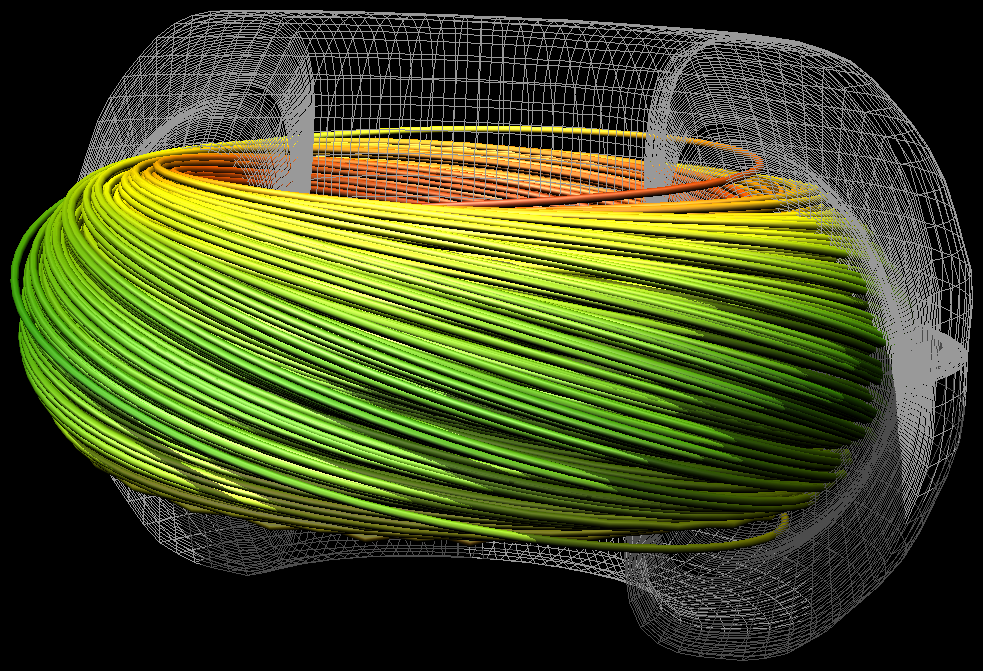
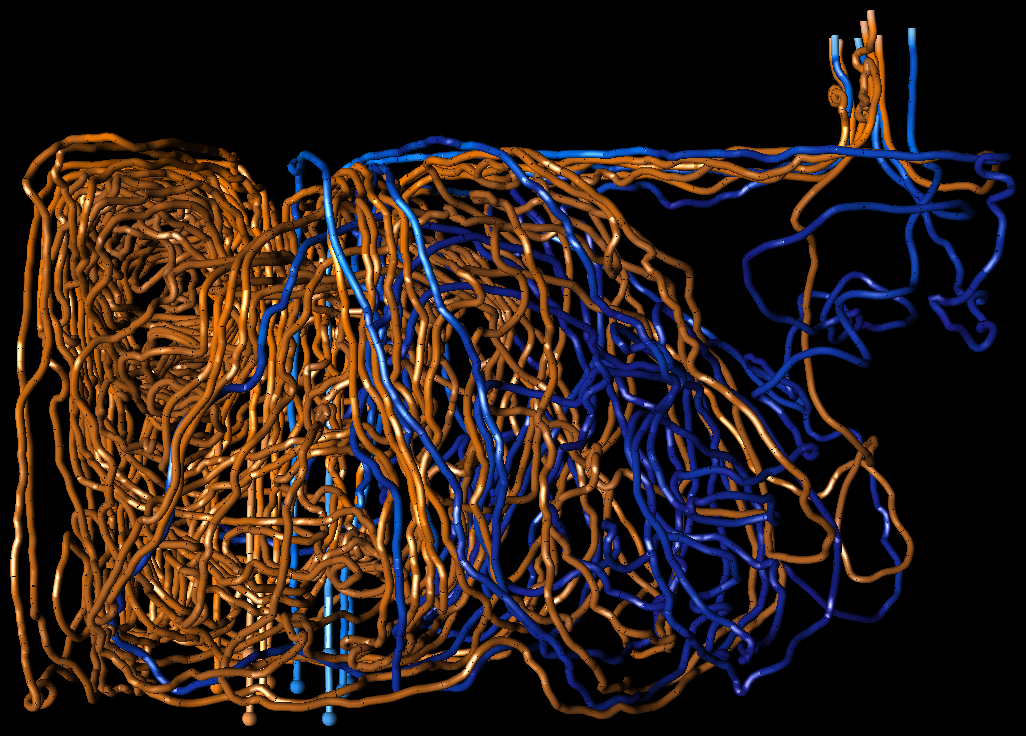
Collaborators
- Dave Pugmoire, ORNL
- Hank Childs, LBNL
- Christoph Garth, UC Davis
- Sean Ahern, ORNL
- Gunther Weber, LBNL