GISProjection
Synopsis
input a data array of latitude, longitudes, and altitudes and output a array of coordinate tuplets after performing a map transformation
Input Port
Output Port
Description
GISProjection takes an n_x 3 Data_Array of Latitude/Longitude/Altitude coordinates and performs a mapping transformation to produce an n x 3 array of (x,y,z) tuplets representing the original coordinates in projected space. The mapping transformation is such that:
f ( lon j , lat j , alt j ) = ( x j , y j , z j )
The mapping transform is specified by user string input to the Transform input port. Currently, only 15 common map transforms are available; those transforms are explained in Transforms .
Input
A port which allows another network component to provide latitude, longitude and altitude information as a Data_Array.
A string specifying the map transformation to be performed on the input data set. The allowed map transforms are listed here, and explained in Transforms :
Several map transformations need access to pieces of information about the space they are projecting into, one of which is the distance from the projection surface to the center of the projection. As these map transformation do their work in three dimensions, the coordinate tuplet (0,0,0) is at the center of the projection space. The GlobalRadius value is the number of units from the surface of the projection to (0,0,0). This value is initially set to 6,378,000 meters, the average distance from the surface of the earth to the center of the earth.
Note: This value can be changed to any non-zero value, but keep in mind that the units represented in this value are the units that will be used throughout the projection network. (e.g. if the value is changed to 6,378 kilometers, all coordinate output from the projection module will be in units of a kilometer.)
Another piece of information that needs to be provided to most map transformations is the center of projection. This is a fixed point on the surface of the projection that becomes the geometric center of the projection. Typically, the base latitude and longitude is defined as the point that cartographer wants to be the least distorted. The default for baseLat and baseLon are the coordinates for Boston, Massachusetts.
On conic projections, the map projection is performed by mapping the coordinates onto the surface of a cone. The size and shape of the cone can be forced to be conceptually secant at two parallels. The resulting projection has distances preserved at these parallels. As conic projections tend to distort distances wildly as you approach either pole (+/- 90 o ), projections of high latitude areas are corrected by adjusting the first and second parallels. Navigational maps used in Alaska, for example, have the first and second parallels set to 55 o and 65 o . This produces a relatively distortion free projection of the state.
Output Port
Transform
baseLat
baseLon
firstPar
secondParThese ports correspond exactly to the corresponding input ports. They are provided merely as a convenience for passing parameter information to other modules.
Transforms
The GIS tools in AVS/Express do not include all available map transformations, only common transformations that are used widely in various industries for cartographic purposes, and map transformations that are of historical interest. This section discusses each of the map transformation available via the GISProjection module. For a reference for map transformation equations that were used in designing this module, please see Map Projections Used by the U.S. Geological Survey, Geological Survey Bulletin 1532 by John P. Snyder.
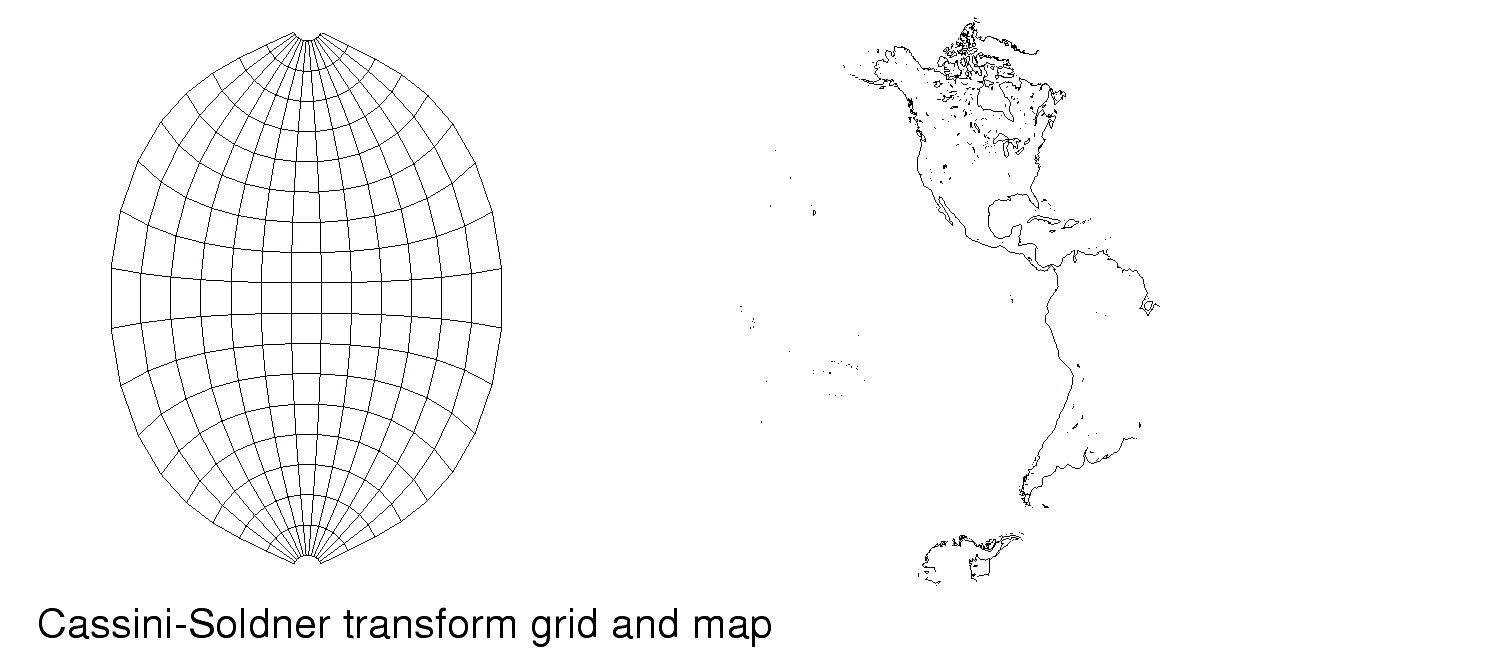
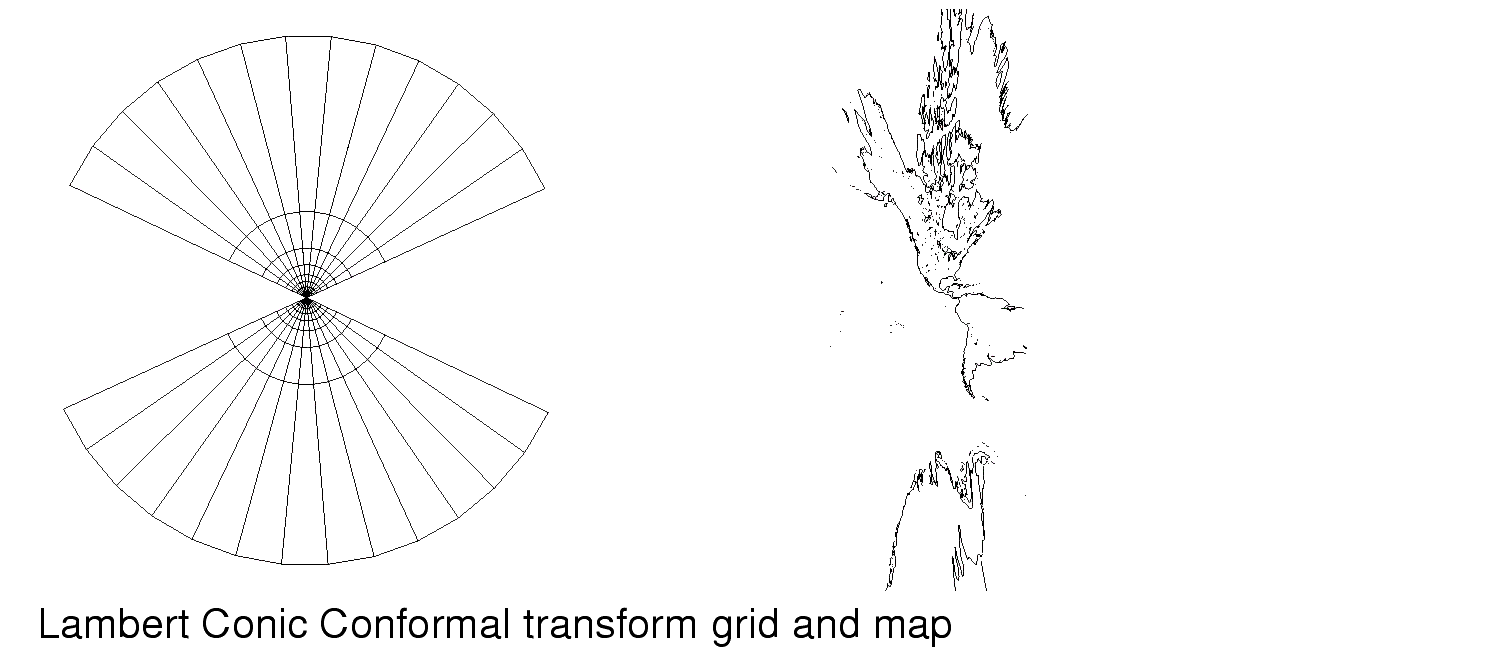
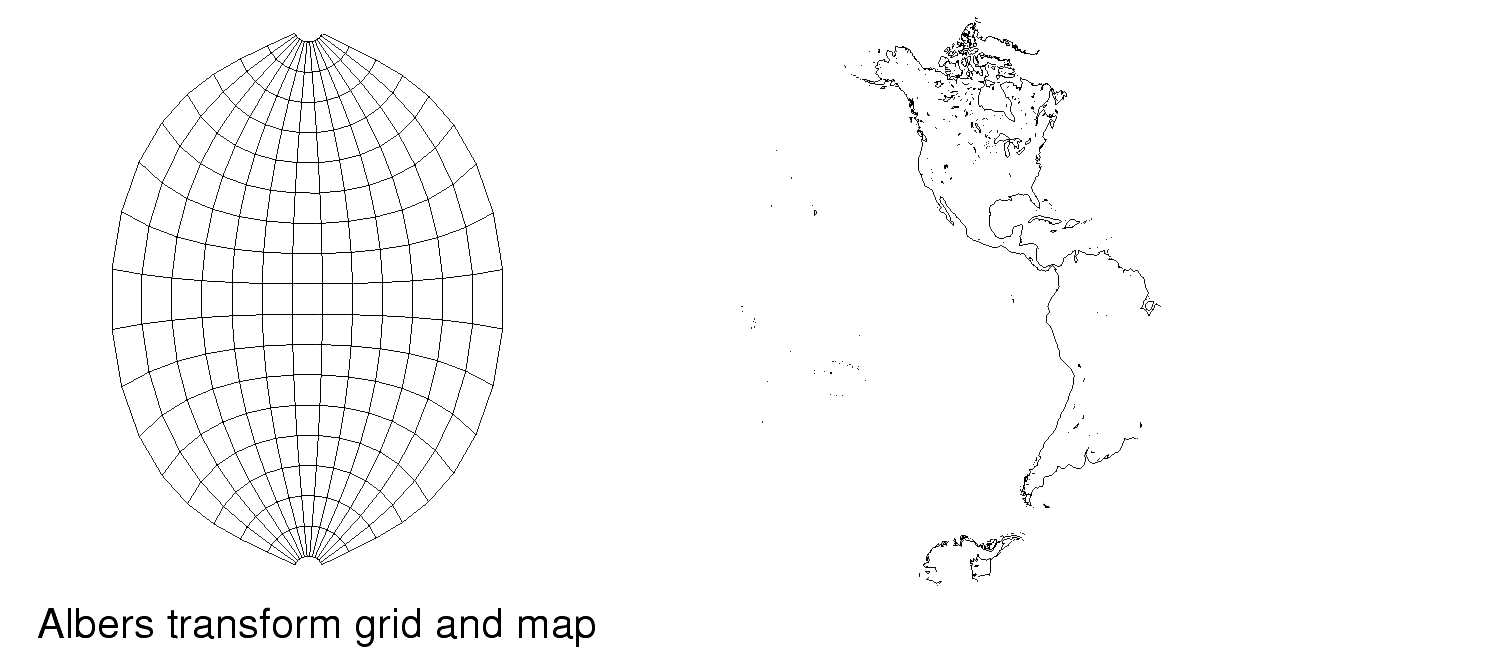
In the sections that follow, a figure showing the grid associated with each transform provided by GISprojection and a map generated using that transform are included.
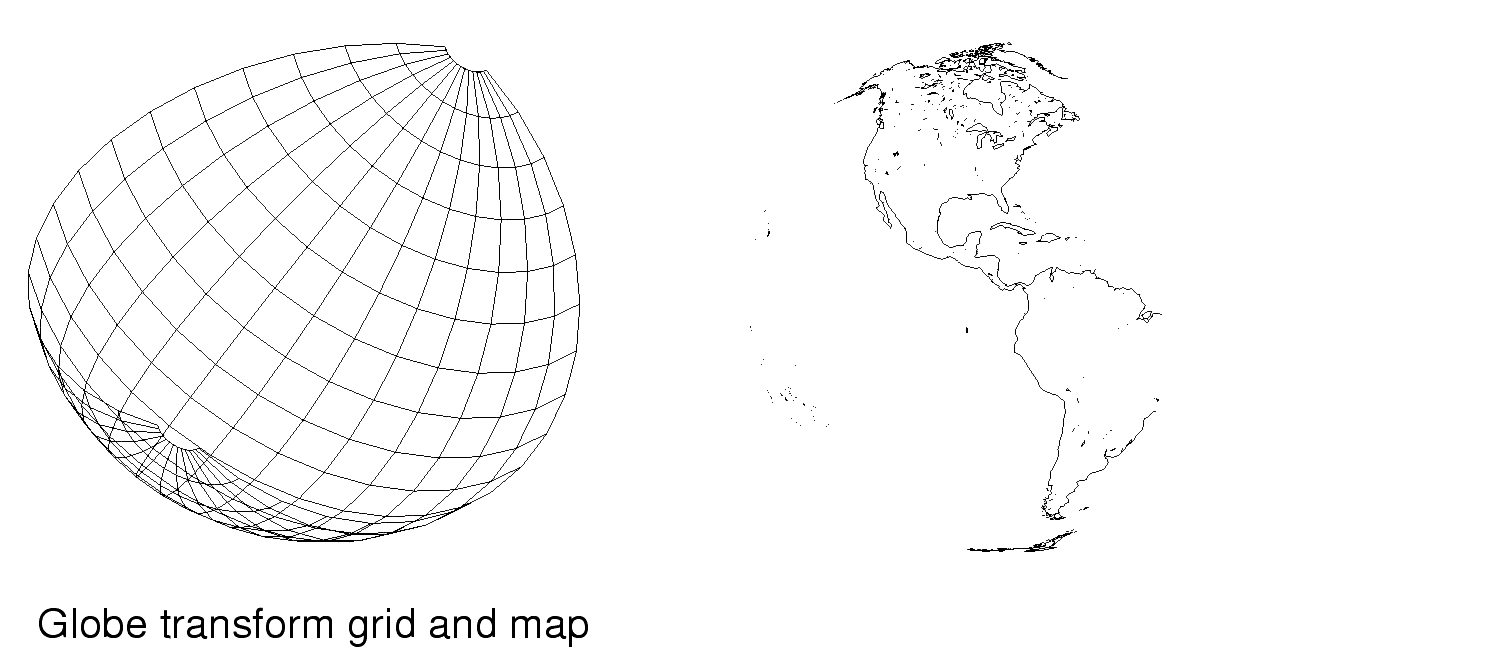
Projection Classification: Sphere
A spherical map transformation is the only true 1-1 mapping of positions on a spherical body to corresponding positions on a representation Parallels are parallel and equally spaced along the meridians. Meridians and other arcs of the great circles are straight lines. Meridians properly converge towards the poles and are spaced the same as parallels at the equator. On spherical projections, the shortest distance between any two surface points is a great circle.
The Spherical Transform provided with GISProjection is Globe
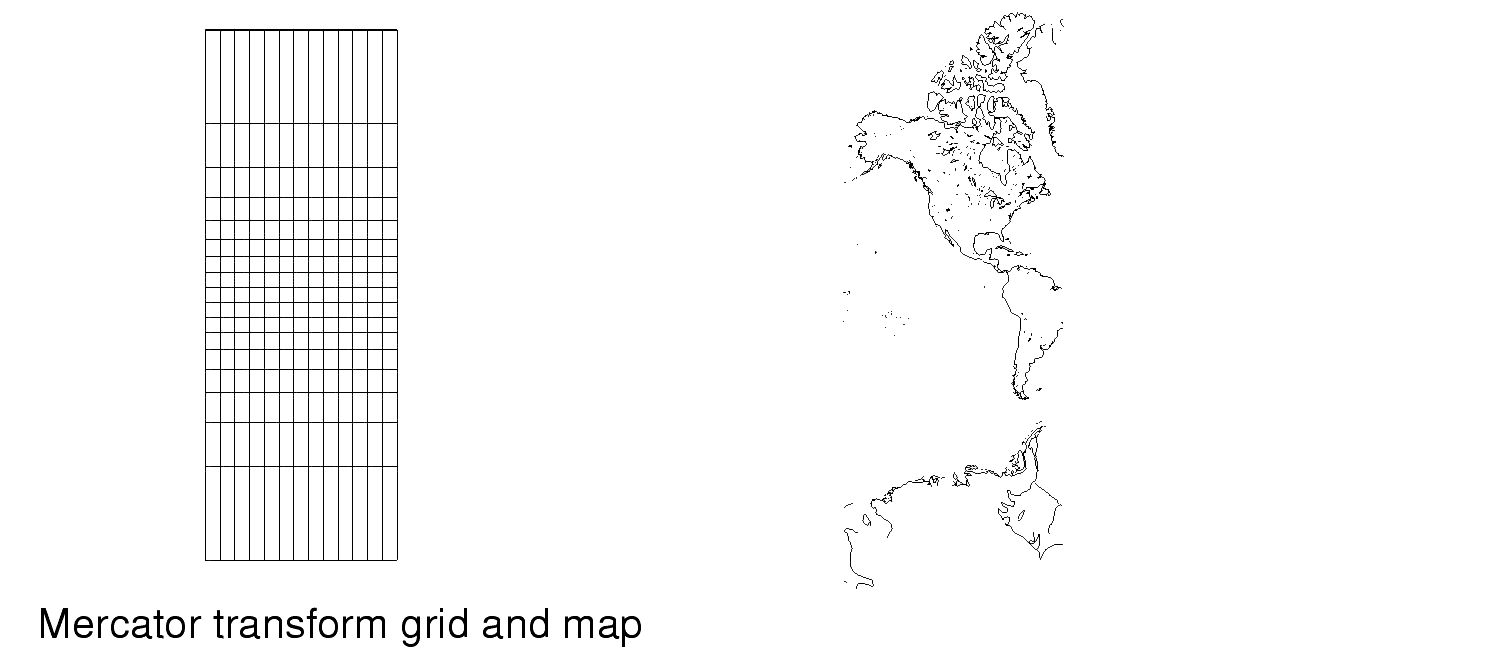
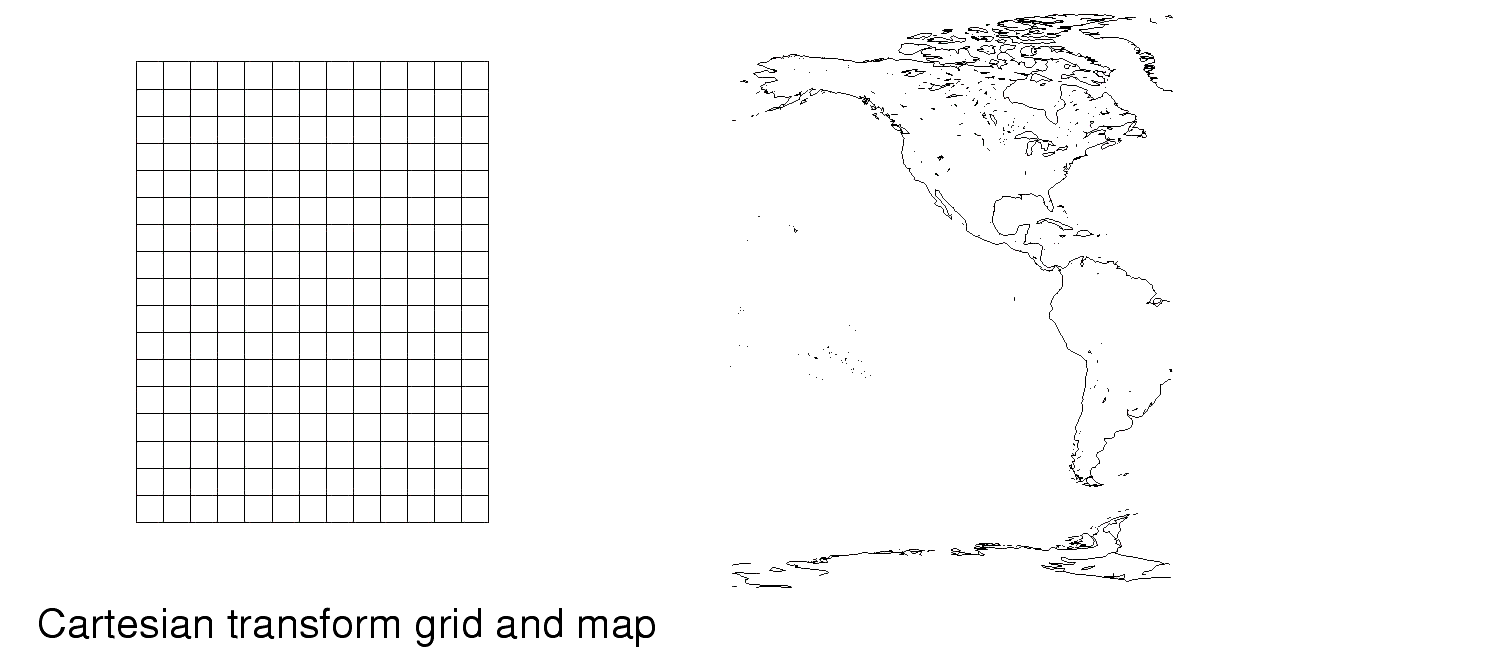
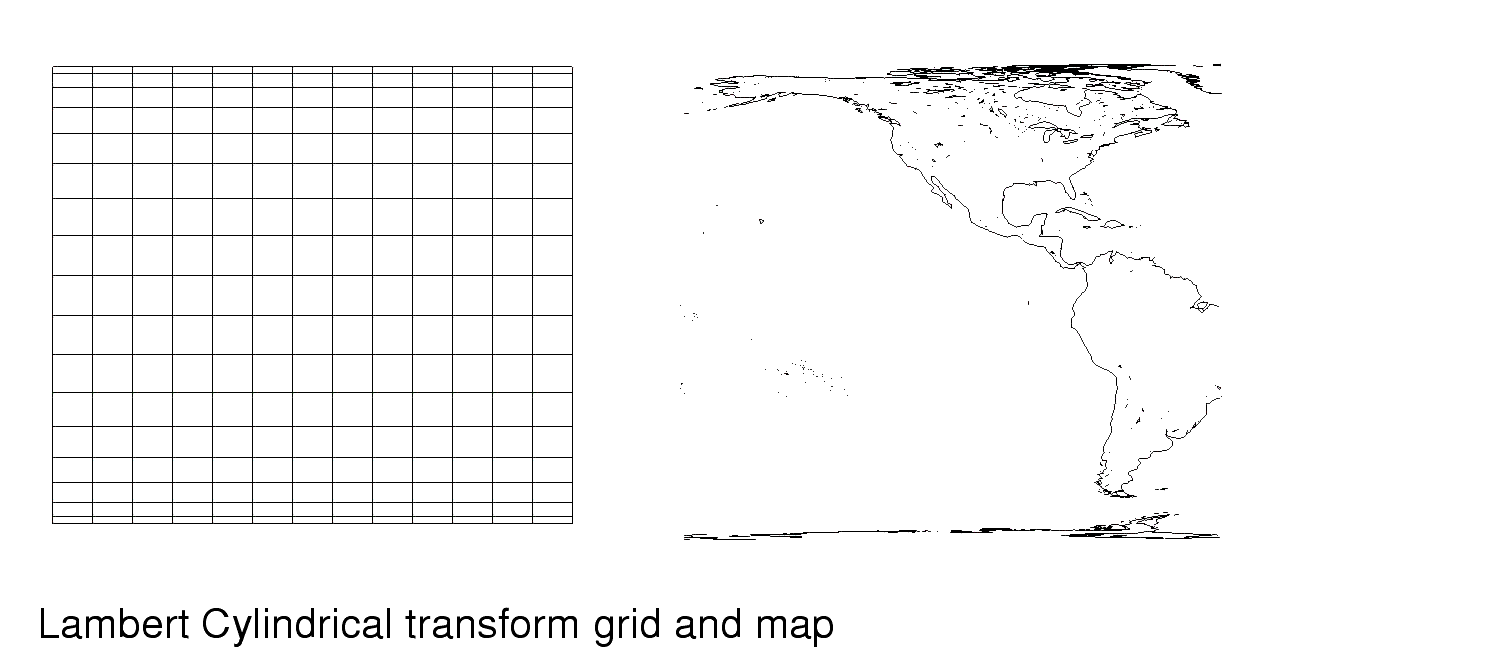
Projection Classification: CylindricalA cylindrical representation of a spherical body is constructed by wrapping a cylinder around the sphere tangent or secant to the a great circle on the surface of the sphere. Points on the sphere are mapped directly onto the cylinder so that the projection line is perpendicular to the surface of the cylinder. Distances are true only along the great circle chosen to be tangential to the cylinder. Distortion of areas increase dramatically as the project gets further from the great circle. Points 90 o from the great circle cannot be represented on the cylindrical projection, as the corresponding projected point maps to infinity.
t Cylindrical Transforms Provided with GISProjection:
Mercator
Cartesian
Lambert Cylindrical
Cassini-Soldner
Projection Classification: Azimuthal
Azimuthal projections are used for prospective mappings of the earth or the other planets. An azimuth angle is formed between one line radiating from chosen central point and another reference line from the same central point. The projection is formed from the intersection of the line and a plane that is tangent to the sphere at the intersection of the reference line. Orthographic projections use the center of the spherical body being mapped as the central point, while stereographic projections use a point on the sphere that is opposite the point of tangency. Directions are true only from the center of the point of projection, and area distortion increases as the projection travels further away from the projection point.
Azimuthal Projections provided with GISProjection:
Conic projections are created by wrapping a cone around the spherical body that is either tangent at one parallel or conceptually secant at two parallels. The parallel are chosen by the cartographer. (All GISProjection conic transforms can be given either one or two parallels. If only one is given, the cone is tangent to the sphere, if two are given, the parallels are used to create conceptual secants to the sphere.) Conic projections are useful in preserving areas around the middle latitudes. Distances are true only along all the meridians and along the one or two chosen parallels. Distortion increases dramatically away from the standard parallel.
Conic Projections provided with GISProjection:
Albers
Projection Classification: Sinusoidal
Although most sinusoidal projections are considered obsolete for navigation purposes, as they produce a discontinuous projection surface in an effort to maintain equal area across the sphere, the sinusoidal projections are still used frequently to show distribution patterns across a sphere. (that is, population figures, oil distribution, and so on) Like cylindrical projections, sinusoidal projections are formed by wrapping a cylinder around the spherical body tangent to the equator. However, unlike cylindrical, attempts to maintain equal areas across the project result in discontinuities or severe shape distortions. For this reason. the projection is also called either Pseudocylindrical or Mercator Equal-Area. Distances are correct along all parallels and the tangential meridian.
Sinusoidal Projections Provided in GISProjection:
Example
File
See also related modules